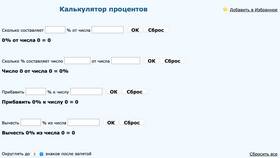
Решение задач на проценты - важный навык, который применяется в математике, экономике и повседневной жизни. Рассмотрим основные типы задач и методы их решения.
Содержание
Основные понятия
- Процент - сотая часть числа (1% = 1/100 = 0,01)
- База - число, от которого вычисляются проценты
- Процентная ставка - величина процентов
- Прирост - увеличение значения на определенный процент
- Скидка - уменьшение значения на определенный процент
Типы задач и методы решения
Нахождение процента от числа
Формула: Результат = (Число × Процент) / 100
| Пример | Найти 15% от 200 |
| Решение | (200 × 15) / 100 = 30 |
Нахождение числа по его проценту
Формула: Число = (Часть × 100) / Процент
| Пример | Число, 25% которого равны 50 |
| Решение | (50 × 100) / 25 = 200 |
Нахождение процентного соотношения
Формула: Процент = (Часть / Целое) × 100%
| Пример | Сколько процентов составляет 3 от 12? |
| Решение | (3 / 12) × 100% = 25% |
Сложные задачи
Последовательное изменение процентов
При последовательном увеличении/уменьшении на несколько процентов:
- Перевести проценты в множители (1 + p/100)
- Перемножить все множители
- Вычесть 1 и умножить на 100% для конечного процента
Задачи на смеси и растворы
Формула для расчета конечной концентрации:
C = (m₁p₁ + m₂p₂) / (m₁ + m₂)
где m - масса, p - процентное содержание
Практические советы
- Внимательно читайте условие задачи
- Определяйте, что является базой для расчета
- Проверяйте размерность получаемых величин
- Для сложных задач делайте промежуточные вычисления
- Используйте пропорции для проверки решения
Примеры из реальной жизни
| Ситуация | Решение |
| Расчет скидки в магазине | Цена × (100% - % скидки) |
| Начисление банковских процентов | Сумма × (1 + процент/100)n |
| Расчет налога | Доход × процент налога |
Освоив основные методы решения задач с процентами, вы сможете легко применять эти знания в учебе и повседневной жизни.